El siguiente código en el software R nos brinda una forma sencilla para comprobar el teorema del límite central, explícitamente para verificar la distribución muestral de la media muestral. Como puede ver tiene distintas opciones de escoger la distribución, sin necesidad de asumir la normalidad, pero las variables \(x_i\) si deben ser independientes e identicamente distribuidas. Los resultados son asombrosos para quien nunca hizo la prueba bajo simulación ya que, incluso bajo la distribución poblacional más sesgada, no se rechaza que  la media muestral (promedio) se distribuya como una distribución normal con un nivel de significancia \(0.05\) .

# http://www.stat.ucl.ac.be/ISdidactique/Rhelp/library/nortest/html/00Index.html
# el link anterior es para pruebas de normalidad
library(nortest)
N = 3000
#x=rnorm(N,0,1000)
#x=rpois(N, lambda=3)
#x=rbinom(N, 20, .2)
#x=rgamma(N, shape=50/2, rate = 1, scale = 2) # chi cuadrado con k=5
x = rgamma(N, shape = 1, rate = 1) # gamma se rechaza
#x=rgamma(N, shape=1, rate = 1, scale = 5) # exponencial con media 5 se rechaza
#x=runif(N)
#x=rweibull(n=200,shape=2.1,scale=1.1)
mex = c()
w = 0
n = 30
for (i in 1:1000){
  mex[i] = mean(sample(x, n, replace = FALSE))
#setdiff() para comparar dos muestras podria implementarse un codigo para que no se repitan las muestras
#aunque primero tendria que ordenarse las muestra para aplicar esta función
}
layout(matrix(1:2,1,2))
hist(x, main = "Histograma de la población")
hist(mex, main = "Histograma del promedio")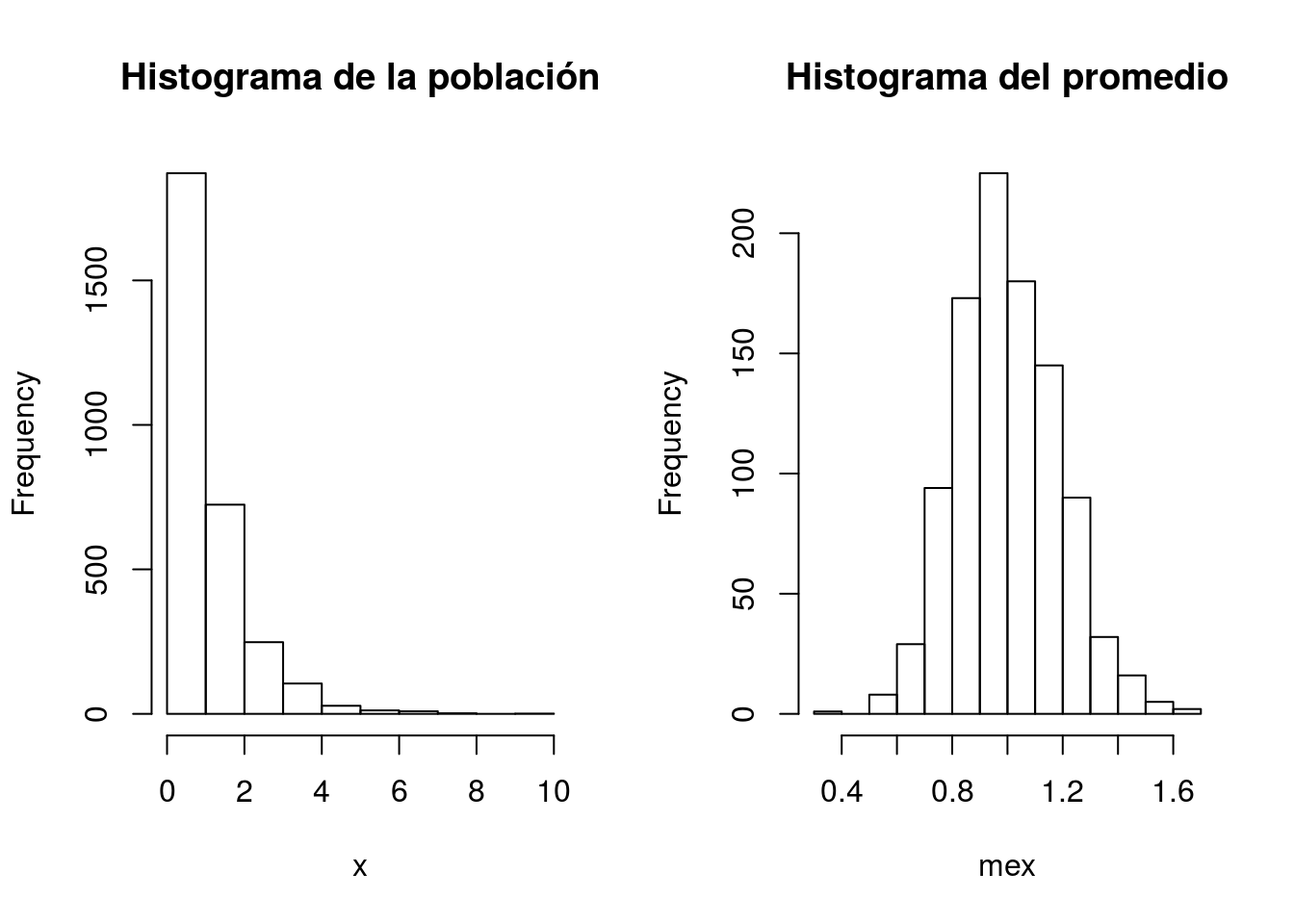

lillie.test(mex) # prueba de kolgomorov

## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  mex
## D = 0.040319, p-value = 0.0006034