Advanced features

In this vignette we present additional features of the sfclust package.

Packages

We begin by loading the required packages.

library(sfclust)
library(stars)
library(ggplot2)
library(dplyr)
library(ggraph)

Data

The simulated dataset used in this vignette, stgaus, is included in our package. It is a stars object with one variable, y, and two dimensions: geometry and time. The dataset represents the number of cases in 100 regions, observed daily over 91 days, starting in January 2024.

data("stgaus")
stgaus

#> stars object with 2 dimensions and 1 attribute
#> attribute(s):
#>         Min.    1st Qu.    Median          Mean   3rd Qu.     Max.
#> y  -1.170275 -0.2390084 0.0302046 -0.0004274323 0.2095926 1.370593
#> dimension(s):
#>          from  to     offset  delta refsys point
#> geometry    1 100         NA     NA     NA FALSE
#> time        1  91 2024-01-01 1 days   Date FALSE
#>                                                                 values
#> geometry POLYGON ((59.5033 683.285...,...,POLYGON ((942.7562 116.89...
#> time                                                              NULL

To gain some initial insights, we can aggregate the data weekly:

stweekly <- aggregate(stgaus, by = "week", FUN = mean)
ggplot() +
    geom_stars(aes(fill = y), stweekly) +
    facet_wrap(~ time, ncol = 5) +
    scale_fill_distiller(palette = "RdBu") +
    theme_bw()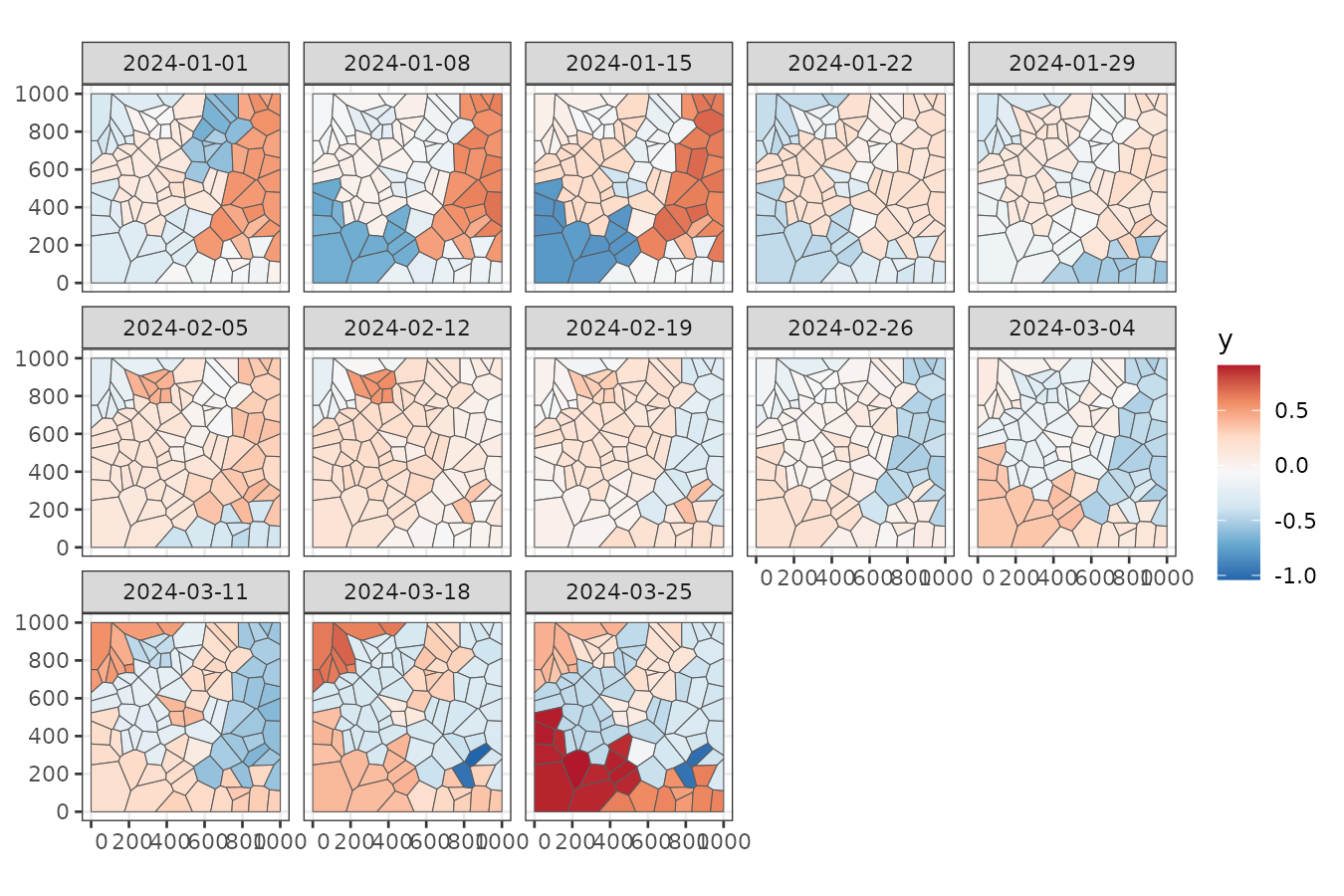

We can also examine the trends for each region:

stgaus |>
    st_set_dimensions("geometry", values = 1:nrow(stgaus)) |>
    as_tibble() |>
    ggplot() +
    geom_line(aes(time, y, group = geometry, color = factor(geometry)), linewidth = 0.3) +
    theme_bw() +
    theme(legend.position = "none")

Some regions exhibit similar trends over time, but the overall patterns are more complex than polinomial functions. Our goal is to cluster these regions while accounting for spatial contiguity.

Clustering

Model

We assume that the response variable $Y_{it}$ for region $i$ at time $t$ follows a normal distribution given the partition $M$ : $Y_{it} \mid \mu_{it}, M \stackrel{ind}{\sim} \text{Normal}(\mu_{it}, \sigma^2),$ where the mean $\mu_{it}$ is modeled based on the cluster assignment $c_i$ : $\mu_{it} = \alpha_{c_i} + f_{c_i,t},$ where $\alpha_{c_i}$ is the intercept for cluster $c_i$ , and $f_{c_i,t}$ is a latent random effect modeled as a random walk process. Specifically, we impose the condition: $f_{c_i,t} - f_{c_i,t-1} \sim N(0, \nu^{-1}), \quad \text{for } t = 2, \dots, n.$

The prior for the hyperparameter $\nu_c$ is defined as: $\log(\nu_c) \sim \text{Normal}(-2, 1).$

Initial clustering

sfclust uses an undirected graph to represent connections between regions and proposes spatial clusters using this graph through minimum spanning trees (MST). By default, sfclust accepts the argument graphdata, which should include:

An undirected igraph object representing spatial connections,
An MST of that graph, and
A membership vector indicating the initial cluster assignments for each region.

For simplicity, you can use the genclust function to generate an initial random partitioning with a specified number of clusters. In this example, we create a partition with 20 clusters:

set.seed(123)
regions <- st_geometry(stgaus)
initial_cluster <- genclust(regions, nclust = 20)
names(initial_cluster)

#> [1] "graph"      "mst"        "membership"

Now, let’s visualize how the regions were randomly clustered:

gg1 <- ggraph(initial_cluster$graph, layout = st_coordinates(st_centroid(st_geometry(stgaus)))) +
    geom_edge_fan(linetype = 1, color = 2) +
    geom_node_point(size = 1.5, color = 1) +
    geom_sf(data = st_geometry(stgaus), fill = NA, color = 1, linewidth = 0.5) +
    labs(subtitle = "(A)") +
    theme_void()
gg2 <- ggraph(initial_cluster$mst, layout = st_coordinates(st_centroid(st_geometry(stgaus)))) +
    geom_edge_fan(linetype = 1, color = 2) +
    geom_node_point(size = 1.5, color = 1) +
    geom_sf(data = st_geometry(stgaus), fill = NA, color = 1, linewidth = 0.5) +
    labs(subtitle = "(B)") +
    theme_void()
gg3 <- st_sf(st_geometry(stgaus), cluster = factor(initial_cluster$membership)) |>
  ggplot() +
    geom_sf(aes(fill = cluster), color = 1) +
    labs(subtitle = "(C)") +
    theme_void() +
    theme(legend.position = "none")
gg1 + gg2 + gg3 & theme(plot.margin = margin(0, 0, 0, 0))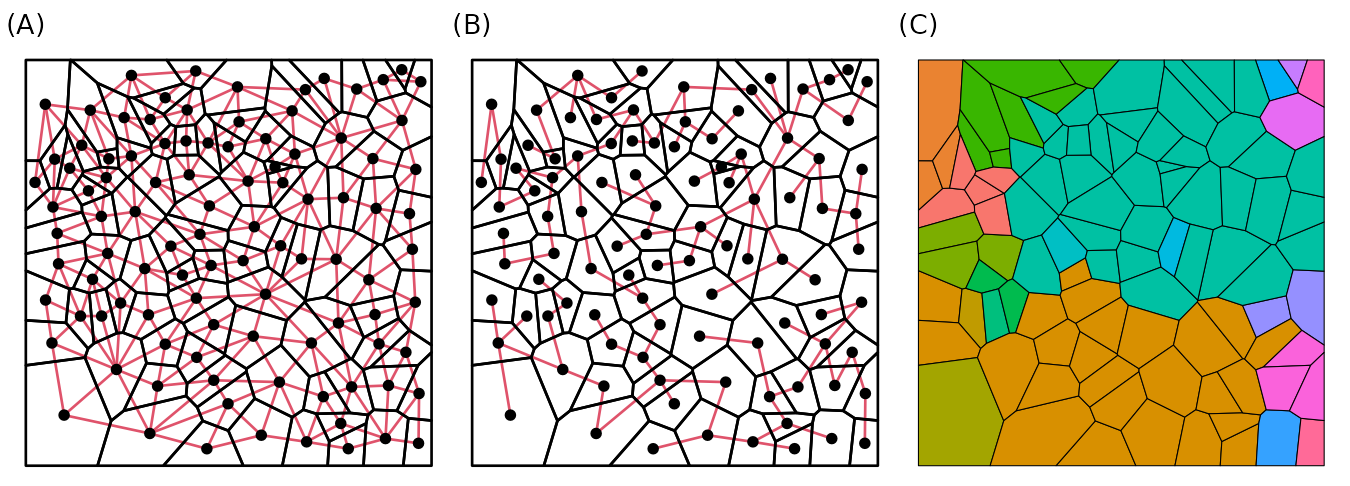

Sampling with `sfclust`

We will initiate the Bayesian clustering algorithm using our generated partition (initial_cluster). Additionally, we use the capabilites of INLA::inla to define a model that includes a random walk process in the linear predictor, and custom priors for the scale hyperparameter. To begin, we will run the algorithm for only 50 iterations.

form <- y ~ f(idt, model = "rw1",
  hyper = list(prec = list(prior = "normal", param = c(-2, 1)))
)
result0 <- sfclust(stgaus, graphdata = initial_cluster, formula = form,
  logpen = -50, niter = 50, burnin = 10, thin = 2, nmessage = 10,
  path_save = file.path("inst", "vigdata", "full-gaussian-mcmc1.rds")
)
result0

#> Within-cluster formula:
#> y ~ f(idt, model = "rw1", hyper = list(prec = list(prior = "normal", 
#>     param = c(-2, 1))))
#> 
#> Clustering hyperparameters:
#> log(1-q)    birth    death   change    hyper 
#>  -50.000    0.425    0.425    0.100    0.050 
#> 
#> Clustering movement counts:
#>  births  deaths changes  hypers 
#>      10       3       1       6 
#> 
#> Log marginal likelihood (sample 20 out of 20): 2335.767

The output indicates that after starting with 20 clusters, the algorithm created 11 new clusters (births), removed 6 clusters (deaths), changed the membership of 3 clusters, and modified the minimum spanning tree (MST) 3 times.

The plot method allows us to select which graph to produce. For example, we can visualize only the log marginal likelihood to diagnose convergence. With just 50 iterations, we can see that the log marginal likelihood has not yet achieved convergence.

plot(result0, which = 3)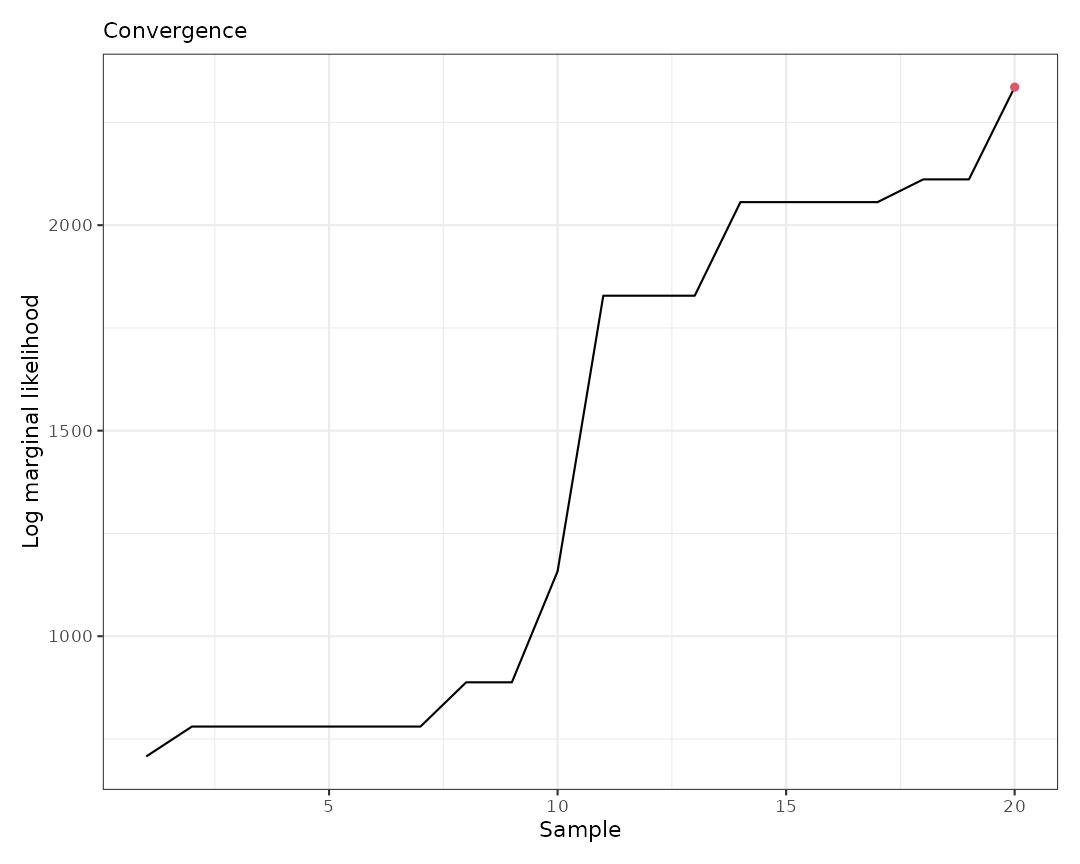

Continue sampling

To achieve convergence, we can continue the sampling using the update function and specify the number of new iterations with the niter argument:

result <- update(result0, niter = 1000)
result

#> Within-cluster formula:
#> y ~ f(idt, model = "rw1", hyper = list(prec = list(prior = "normal", 
#>     param = c(-2, 1))))
#> 
#> Clustering hyperparameters:
#> log(1-q)    birth    death   change    hyper 
#>  -50.000    0.425    0.425    0.100    0.050 
#> 
#> Clustering movement counts:
#>  births  deaths changes  hypers 
#>      34      50      15      56 
#> 
#> Log marginal likelihood (sample 1000 out of 1000): 12654.03

With 2000 additional iterations, there have been many clustering movements. Furthermore, when visualizing the results, we can observe that the log marginal likelihood has achieved convergence.

plot(result, which = 3)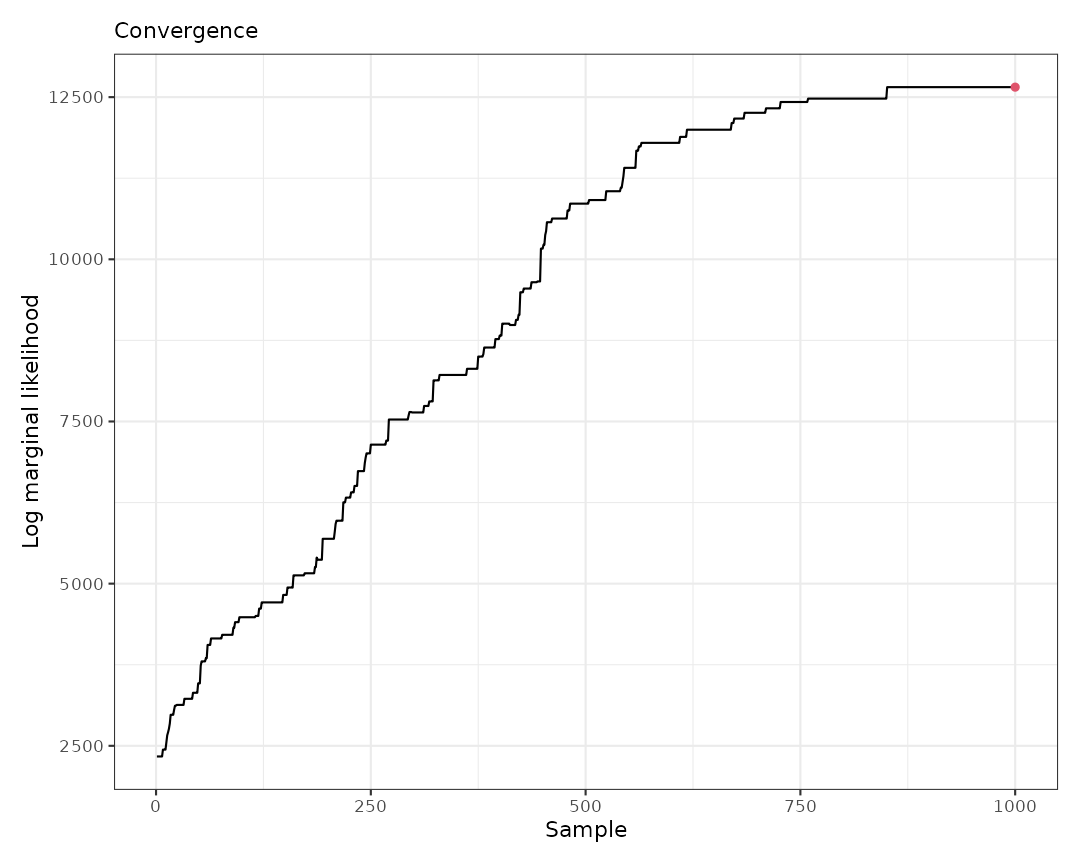

gg1 <- plot(result0, which = 3) + labs(subtitle = "(A)")
gg2 <- plot(result, which = 3) + labs(subtitle = "(B)")
gg1 + gg2

if (save_figures) {
  ggsave(file.path(path_figures, "stgaus-marginal-likelihood.pdf"), width = 10, height = 4.5,
    device = cairo_pdf)
}

result_other <- sfclust:::update_within(result, sample = 750)
result_other

#> Within-cluster formula:
#> y ~ f(idt, model = "rw1", hyper = list(prec = list(prior = "normal", 
#>     param = c(-2, 1))))
#> 
#> Clustering hyperparameters:
#> log(1-q)    birth    death   change    hyper 
#>  -50.000    0.425    0.425    0.100    0.050 
#> 
#> Clustering movement counts:
#>  births  deaths changes  hypers 
#>      34      50      15      56 
#> 
#> Log marginal likelihood (sample 750 out of 1000): 12425.03

Results

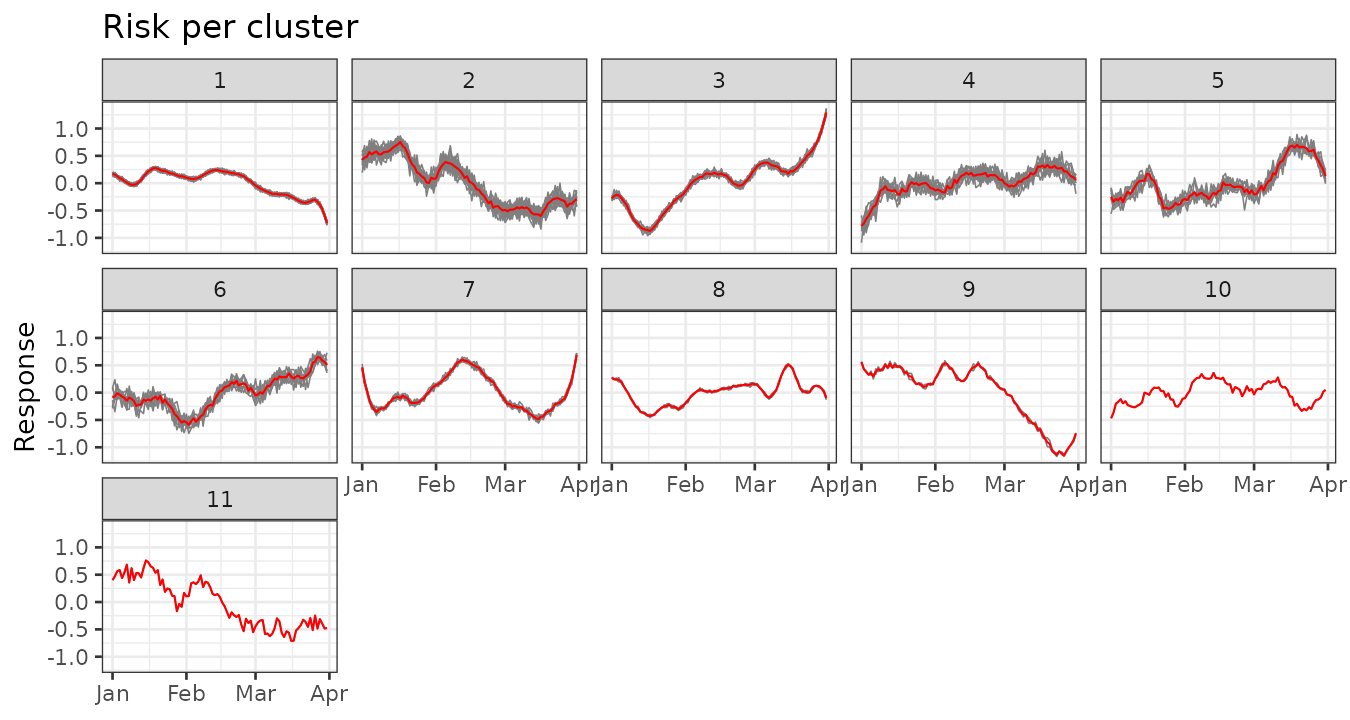
The final iteration indicates that the algorithm identified 10 clusters, with a log marginal likelihood of 12,708.35. The largest cluster consists of 27 regions, while the smallest contains only one region.

summary(result, sort = TRUE)

#> Summary for clustering sample 1000 out of 1000 
#> 
#> Within-cluster formula:
#> y ~ f(idt, model = "rw1", hyper = list(prec = list(prior = "normal", 
#>     param = c(-2, 1))))
#> 
#> Counts per cluster:
#>  1  2  3  4  5  6  7  8  9 10 11 
#> 27 19 12 11  9  9  6  3  2  1  1 
#> 
#> Log marginal likelihood:  12654.03

Let’s visualize the regions grouped by cluster.

plot(result, which = 1:2, sort = TRUE, legend = TRUE)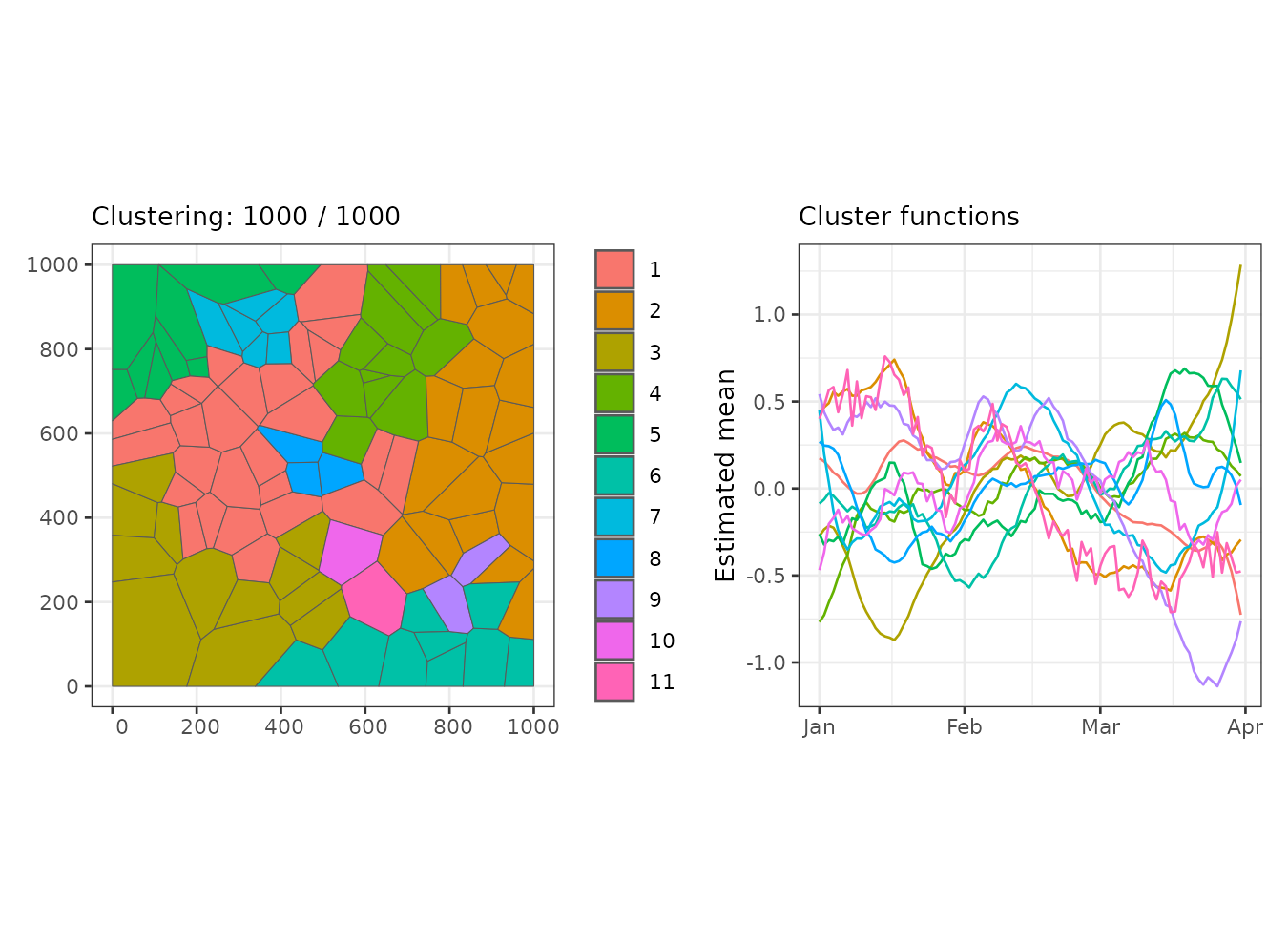

Let’s visualize the original data grouped by cluster.

plot_clusters_series(result, y, sort = TRUE) +
  facet_wrap(~ cluster, ncol = 5) +
  labs(title = "Risk per cluster", y = "Response")